2023. 11. 4. 15:26ㆍ파이썬(Python)
1. 사각형 넓이 구하기
- 예를 들어 좌표 (2, 3)과 (5, 7)이 각각 사각형의 좌측 하단과 우측 상단의 좌표일 때 넓이를 구해야 한다.

- 수식을 사용하면 가로 3 (=5-2), 세로 4 (=7-3)이기 때문에 넓이는 12이다.
- 다른 방법으로는 2차원 배열을 이용하는 것이다.
- 두 모서리가 (2, 3), (5, 7)이므로 배열의 2행 3열, 5행 7 열이라 생각한다.
- 2차원 배열이 8행 8열이 있다고 가정하고 모든 원소는 0이다.
- 이중 반복문을 사용해 2행 3열부터 5행 7열에서 각각 1행 1열을 뺀 4행 6열까지 순회한다.
- 순회하며 개수를 하나씩 증가한다.
- 총개수가 사각형의 넓이가 된다.
- 따라서 좌측 하단 모서리가 (x1, y1)이고 우측 상단 모서리가 (x2, y2)인 직사각형의 넓이는 2차원 배열에서 x1행 y1열부터 x2-1행 y2-1열까지 순회한 개수가 된다.
x1, y1 = map(int, input().split())
x2, y2 = map(int, input().split())
rectangle = [[0 for _ in range(8)] for _ in range(8)]
cnt = 0
for i in range(x1, x2):
for j in range(y1, y2):
cnt += 1
print(cnt)
>> 2 3
>> 5 7
12
- 좌표에 음수가 있다면 어떻게 해야 할까?
- 예를 들어 좌측 하단과 우측 상단에 각각 (-2, -3), (3, -2)의 직사각형이 있다고 하자.
- 배열은 음수 인덱스를 가질 수 없기 때문에 특정 offset를 더해 0 또는 양수로 만든다.
- 위의 경우 모든 좌표에 3을 더하면 (1, 0), (6, 1)을 사용해서 문제를 푼다.
2. 2차원 배열을 이용한 사각형 넓이 구하기 코드 구현
2-1. 변수 지정
n = int(input()) # 사각형 개수
min_x, min_y = sys.maxsize, sys.maxsize # n개의 사각형 중 x 좌표와 y 좌표의 최솟값
max_x, max_y = -sys.maxsize, -sys.maxsize # n개의 사각형 중 x 좌표와 y 좌표의 최솟값
arr = [] # (x1, y1, x2, y2) 형식의 원소를 가지는 배열 (리스트)
offset_x, offset_y = 0, 0 # 좌표가 음수가 나올 수 있으므로 offset 설정
- min_x, min_y는 음수일 경우, offset을 설정하기 위해 구한다.
- max_x, max_y는 2차원 배열의 크기를 지정하기 위해 구한다.
- 좌측 하단의 좌표, 우측 상단의 좌표의 데이터를 가진 사각형을 튜플로 저장할 리스트를 설정한다.
- offset을 각각 x, y로 나누어 구한다.
2-2. 좌표 입력 및 최소, 최대 구하기
for _ in range(n):
x1, y1, x2, y2 = map(int, input().split())
min_x, min_y = min(x1, min_x), min(y1, min_y)
max_x, max_y = max(x2, max_x), max(y2, max_y)
arr.append((x1, y1, x2, y2))
- (x1, y1)은 좌측 하단, (x2, y2)는 우측 상단 좌표이다.
- x1 < x2, y1 < y2를 만족한다.
- x, y의 최솟값은 n개의 x1과 y1에서 최댓값은 n개의 x2와 y2에서 나온다.
2-3. offset과 2차원 배열 크기 조정.
if min_x < 0:
max_x += abs(min_x)
offset_x += abs(min_x)
if min_y < 0:
max_y += abs(min_y)
offset_y += abs(min_y)
- min_x 또는 min_y가 음수이면 배열은 음수의 인덱스를 가질 수 없기 때문에 0 이상의 양수로 나타내야 한다.
- min_x가 음수이면 max_x와 offset_x에 양수 min_x를 더한다.
- min_y가 음수이면 max_y와 offset_y에 양수 min_y를 더한다.
- 음수가 아니라면 offset은 0이고 2차원 배열의 크기는 변하지 않는다.
2-4. 2차원 배열 생성과 사각형의 넓이 구하기.
checked = [[False for _ in range(max_y+1)] for _ in range(max_x+1)]
cnt = 0 # 직사각형 넓이
for x1, y1, x2, y2 in arr:
for i in range(x1+offset_x, x2+offset_x):
for j in range(y1+offset_y, y2+offset_y):
cnt += 1
- max_x행 max_y열의 2차원 배열을 생성한다.
- n개의 사각형의 좌표를 순회하면서 x좌표는 offset_x를 더하고, y좌표는 offset_y를 더한다.
- 이중 반복문에서 문제에 맞는 조건을 넣어 다양한 문제를 구할 수 있다.
Q) 사각형의 총 넓이
- n개의 직사각형의 총넓이를 구하라.
- 입력은 사각형 1개당 좌측 하단의 좌표와 우측 상단의 좌표를 입력한다.

import sys
n = int(input()) # 사각형 개수
min_x, min_y = sys.maxsize, sys.maxsize # n개의 사각형 중 x 좌표와 y 좌표의 최솟값
max_x, max_y = -sys.maxsize, -sys.maxsize # n개의 사각형 중 x 좌표와 y 좌표의 최솟값
arr = [] # (x1, y1, x2, y2) 형식의 원소를 가지는 배열 (리스트)
offset_x, offset_y = 0, 0 # 좌표가 음수가 나올 수 있으므로 offset 설정
for _ in range(n):
x1, y1, x2, y2 = map(int, input().split())
min_x, min_y = min(x1, min_x), min(y1, min_y)
max_x, max_y = max(x2, max_x), max(y2, max_y)
arr.append((x1, y1, x2, y2))
if min_x < 0:
max_x += abs(min_x)
offset_x += abs(min_x)
if min_y < 0:
max_y += abs(min_y)
offset_y += abs(min_y)
checked = [[False for _ in range(max_y+1)] for _ in range(max_x+1)]
cnt = 0 # 직사각형 넓이
for x1, y1, x2, y2 in arr:
for i in range(x1+offset_x, x2+offset_x):
for j in range(y1+offset_y, y2+offset_y):
if not checked[i][j]:
checked[i][j] = True
cnt += 1
print(cnt)
>> 3
>> 1 3 5 7
>> 3 5 6 8
>> 4 2 7 6
29
- 이중 반복문을 통해 이중 배열의 i행 j열의 개수에 따라 넓이를 구할 수 있다.
- 초기값을 False로 하고 i행 j열을 지날 때마다 True로 바꾼다.
- 만약 겹치는 구간이 있으면 개수를 중복으로 셀 수 있으므로 False인 경우에만 개수를 센다.
Q) 정사각형의 총 넓이
- n개의 정사각형의 총넓이를 구하라.
- 입력은 좌측 하단의 좌표와 길이를 입력하라.
- 3 3 3이라 입력하면 좌측 하단의 좌표가 (3, 3)이고 길이가 3인 정사각형이다.

import sys
n = int(input()) # 사각형 개수
min_x, min_y = sys.maxsize, sys.maxsize # n개의 사각형 중 x 좌표와 y 좌표의 최솟값
max_x, max_y = -sys.maxsize, -sys.maxsize # n개의 사각형 중 x 좌표와 y 좌표의 최솟값
arr = [] # (x1, y1, x2, y2) 형식의 원소를 가지는 배열 (리스트)
offset_x, offset_y = 0, 0 # 좌표가 음수가 나올 수 있으므로 offset 설정
for _ in range(n):
x, y, length = map(int, input().split())
min_x, min_y = min(x, min_x), min(y, min_y)
max_x, max_y = max(x+length, max_x), max(y+length, max_y)
arr.append((x, y, x+length, y+length))
if min_x < 0:
max_x += abs(min_x)
offset_x += abs(min_x)
if min_y < 0:
max_y += abs(min_y)
offset_y += abs(min_y)
checked = [[False for _ in range(max_y+1)] for _ in range(max_x+1)]
cnt = 0 # 직사각형 넓이
for x1, y1, x2, y2 in arr:
for i in range(x1+offset_x, x2+offset_x):
for j in range(y1+offset_y, y2+offset_y):
if not checked[i][j]:
checked[i][j] = True
cnt += 1
print(cnt)
>> 3
>> 1 4 2
>> 4 3 4
>> 2 5 3
26
- 좌측 하단의 좌표와 길이를 입력하여 이를 이용해 우측 상단의 좌표를 구해야 한다.
- 우측 상단의 좌표는 (좌측 하단의 x좌표+길이, 좌측 하단의 y좌표+길이)이다.
- 나머지 내용은 위의 '사각형의 총 넓이' 문제와 같다.
Q) 장애물로 제거된 넓이
- n개의 사각형을 겹치지 않게 입력한다.
- 사각형의 입력은 좌측 하단의 좌표와 우측 상단의 좌표를 입력한다.
- n개의 사각형을 입력 후 장애물의 사각형을 입력한다.
- n개의 사각형 중 장애물 사각형과 겹친 부분을 제외하고 남은 넓이를 구한다.

import sys
n = int(input()) # 사각형 개수
min_x, min_y = sys.maxsize, sys.maxsize # n개의 사각형 중 x 좌표와 y 좌표의 최솟값
max_x, max_y = -sys.maxsize, -sys.maxsize # n개의 사각형 중 x 좌표와 y 좌표의 최솟값
arr = [] # (x1, y1, x2, y2) 형식의 원소를 가지는 배열 (리스트)
offset_x, offset_y = 0, 0 # 좌표가 음수가 나올 수 있으므로 offset 설정
for _ in range(n):
x1, y1, x2, y2 = map(int, input().split())
min_x, min_y = min(x1, min_x), min(y1, min_y)
max_x, max_y = max(x2, max_x), max(y2, max_y)
arr.append((x1, y1, x2, y2))
obstacle = tuple(map(int, input('장애물의 사각형은? ').split()))
if min_x < 0:
max_x += abs(min_x)
offset_x += abs(min_x)
if min_y < 0:
max_y += abs(min_y)
offset_y += abs(min_y)
checked = [[False for _ in range(max_y+1)] for _ in range(max_x+1)]
cnt = 0 # 직사각형 넓이
for x1, y1, x2, y2 in arr:
for i in range(x1+offset_x, x2+offset_x):
for j in range(y1+offset_y, y2+offset_y):
if not checked[i][j]:
checked[i][j] = True
cnt += 1
xa, ya, xb, yb = obstacle
for i in range(xa+offset_x, xb+offset_x):
for j in range(ya+offset_y, yb+offset_y):
if checked[i][j]:
cnt -= 1
print(cnt)
>> 3
>> 2 1 3 3
>> 1 4 4 7
>> 5 1 7 4
>> 장애물의 사각형은? 2 2 6 6
10
- n개의 사각형을 입력 후 장애물 사각형의 좌측 하단, 우측 상단 좌표를 입력한다.
- n개의 사각형의 넓이를 이중 배열의 개수를 이용해 구한다.
- 장애물 사각형의 튜플 변수를 각각 4개의 숫자 변수로 언패킹 한다.
- 각각 offset을 더해 이중 반복문을 순회한다.
- i행 j열이 True인 곳이 입력한 사각형의 범위이므로 넓이가 포함된다.
- 따라서 True이면 개수를 빼서 전체 사각형의 넓이 중 장애물이 포함된 범위를 뺀 넓이를 구할 수 있다.
Q) 흰색과 검은색의 사각형
- n개의 사각형이 주어진다.
- 처음에 주어진 사각형은 흰색이고, 다음에 주어지는 사각형은 검은색이다.
- 이와 같이 흰색, 검은색, 흰색, 검은색... 순서로 사각형이 주어진다.
- 겹치는 위치는 마지막에 덮인 색으로 한다.
- 이때, 흰색과 검은색의 넓이를 구하여라.
import sys
n = int(input()) # 사각형 개수
min_x, min_y = sys.maxsize, sys.maxsize # n개의 사각형 중 x 좌표와 y 좌표의 최솟값
max_x, max_y = -sys.maxsize, -sys.maxsize # n개의 사각형 중 x 좌표와 y 좌표의 최솟값
arr = [] # (x1, y1, x2, y2) 형식의 원소를 가지는 배열 (리스트)
offset_x, offset_y = 0, 0 # 좌표가 음수가 나올 수 있으므로 offset 설정
for i in range(n):
x1, y1, x2, y2 = map(int, input().split())
min_x, min_y = min(x1, min_x), min(y1, min_y)
max_x, max_y = max(x2, max_x), max(y2, max_y)
if i % 2 == 0:
arr.append((x1, y1, x2, y2, 'w'))
else:
arr.append((x1, y1, x2, y2, 'b'))
if min_x < 0:
max_x += abs(min_x)
offset_x += abs(min_x)
if min_y < 0:
max_y += abs(min_y)
offset_y += abs(min_y)
checked = [[False for _ in range(max_y+1)] for _ in range(max_x+1)]
cnt_w, cnt_b = 0, 0 # 흰색, 검은색 넓이
for x1, y1, x2, y2, color in arr:
for i in range(x1+offset_x, x2+offset_x):
for j in range(y1+offset_y, y2+offset_y):
if color == 'w':
checked[i][j] = 'w'
else:
checked[i][j] = 'b'
for area in checked:
cnt_w += area.count('w')
cnt_b += area.count('b')
print(cnt_w, cnt_b)
>> 2
>> 2 1 7 4
>> 5 -1 10 3
11 20
- 사각형은 흰색, 검은색 순으로 입력이 된다.
- 따라서 0부터 시작하면 짝수번째는 흰색, 홀수번째는 검은색이 되고 리스트에 추가한다.
- 이중 배열을 통해 색깔이 흰색이면 i행 j열에 흰색이 되고, 검은색이면 i행 j열에 검은색이 된다.
- 흰색과 검은색의 넓이를 구하기 위해 이중 리스트의 각 원소인 리스트의 개수를 더한다.
- 흰색인 경우 리스트의 원소에 'w'의 개수를 구해야 하므로 count 함수를 사용한다.
- 검은색도 count를 사용하여 'b'의 개수를 구한다.
3. 최소 직사각형의 넓이
- 다음과 같이 3개의 직사각형이 있을 때, 3개의 직사각형을 포함하는 최소 직사각형의 넓이를 구하라.
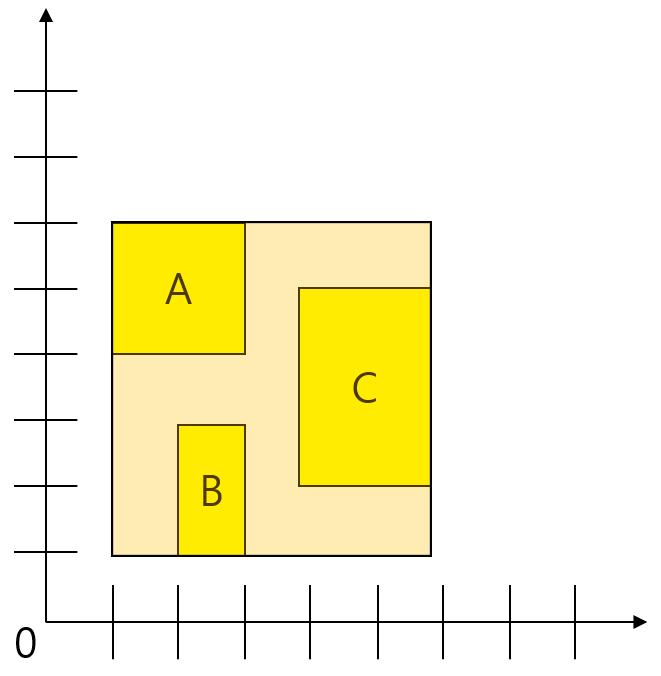
- 사각형 A, B, C가 좌측 하단, 우측 상단의 좌표가 주어지면 각각의 범위 내에 이중 배열에 체크한다.
- 3개의 사각형을 포함하는 최소 직사각형(D)의 좌측 하단, 우측 상단의 좌표를 구해야 한다.
- 위 그림에서는 (A의 좌측 하단 x, B의 좌측 하단 y)가 D의 좌측 하단의 좌표이다.
- (C의 우측 상단의 x, A의 우측 상단의 y)가 D의 우측 상단의 좌표가 된다.
- 따라서 A, B, C의 x좌표 중 최대 최소인 min_x, max_x, y좌표 중 최대 최소인 min_y, max_y를 구한다.
- 따라서 D의 좌측 하단이 (min_x, min_y), 우측 상단이 (max_x, max_y) 일 때, 넓이는 (max_x-min_x) * (max_y-min_y)이 된다.
import sys
n = int(input()) # 사각형 개수
min_x, min_y = sys.maxsize, sys.maxsize # n개의 사각형 중 x 좌표와 y 좌표의 최솟값
max_x, max_y = -sys.maxsize, -sys.maxsize # n개의 사각형 중 x 좌표와 y 좌표의 최솟값
for i in range(n):
x1, y1, x2, y2 = map(int, input().split())
min_x, min_y = min(x1, min_x), min(y1, min_y)
max_x, max_y = max(x2, max_x), max(y2, max_y)
print((max_x-min_x)*(max_y-min_y))
>> 3
>> 1 4 3 6
>> 2 1 3 3
>> 4 2 6 5
25
Q) 싱크홀 공사
- 직사각형 모양으로 싱크홀이 생겼다.
- 직사각형의 모양으로 n개의 싱크홀을 메꾼다.
- 공사가 완료되기 위해 메꿔야 할 직사각형의 최소 넓이를 구하라.


- 위 그림에서 파란색 영역으로 덮이지 않은 검은색 영역 중 직사각형으로 덮을 때 최소 직사각형의 넓이를 구해야 한다.

import sys
arr = [] # (x1, y1, x2, y2) 형식의 원소를 가지는 배열 (리스트)
min_x, min_y = sys.maxsize, sys.maxsize # n개의 사각형 중 x 좌표와 y 좌표의 최솟값
max_x, max_y = -sys.maxsize, -sys.maxsize # n개의 사각형 중 x 좌표와 y 좌표의 최솟값
xa, ya, xb, yb = map(int, input().split())
min_x, min_y = xa, ya
max_x, max_y = xb, yb
obstacle = [(xa, ya, xb, yb)] # 싱크홀 좌표
n = int(input()) # 사각형 개수
offset_x, offset_y = 0, 0 # 좌표가 음수가 나올 수 있으므로 offset 설정
for _ in range(n):
x1, y1, x2, y2 = map(int, input().split())
min_x, min_y = min(x1, min_x), min(y1, min_y)
max_x, max_y = max(x2, max_x), max(y2, max_y)
arr.append((x1, y1, x2, y2))
arr += obstacle
if min_x < 0:
max_x += abs(min_x)
offset_x += abs(min_x)
if min_y < 0:
max_y += abs(min_y)
offset_y += abs(min_y)
checked = [[False for _ in range(max_y+1)] for _ in range(max_x+1)]
min_w, min_h, max_w, max_h = max_x, max_y, 0, 0
for idx, (x1, y1, x2, y2) in enumerate(arr):
for i in range(x1+offset_x, x2+offset_x):
for j in range(y1+offset_y, y2+offset_y):
if idx == n: # 싱크홀 좌표일 때
if not checked[i][j]: # 덮어져 있는 영역이 True. False 영역을 구하는 것이 목표.
min_w, min_h = min(min_w, i), min(min_h, j)
max_w, max_h = max(max_w, i), max(max_h, j)
else: # 싱크홀을 덮는 영역일 때
checked[i][j] = True
if max_w == 0: # 모두 덮여져 있을 때
print(0)
else:
print((max_w-min_w+1)*(max_h-min_h+1))
>> 1 3 5 6
>> 2
>> 3 1 5 4
>> 2 4 5 7
6
- 싱크홀의 좌측 하단 (xa, ya), 우측 상단 (xb, yb)를 입력받는다.
- 좌측 하단의 좌표는 x, y의 최솟값, 우측 상단의 좌표는 x, y의 최댓값이 된다.
- 싱크홀의 좌표를 튜플로 만들어 obstacle 리스트 변수에 삽입한다.
- n개의 싱크홀을 메꾸는 직사각형 좌표를 입력받아 arr에 삽입한다.
- arr에 obstacle을 붙인다. (싱크홀의 좌표 idx는 n이다.)
- enumerate를 통해 좌표값과 index를 이용해 이중 배열에 값을 부여한다.
- idx가 n이 아니면 싱크홀을 덮는 영역이므로 True로 변환한다.
- idx가 n이면 싱크홀이고 덮은 영역이 아닌 False의 좌표를 구해야 한다.
- i행 j열이 False이면 덮어야 하는 직사각형의 x, y의 최대 최솟값을 구한다.
- 이때 초기값은 최솟값은 max_x, max_y, 최댓값은 0으로 한다.
- 덮어야 할 직사각형의 가로는 x의 최댓값에서 x의 최솟값을 빼고 1을 더한다.
- 세로는 y의 최댓값에서 y의 최솟값을 빼고 1을 더한다.
- 가로와 세로를 곱해 넓이를 구한다.
- 만약 덮어야 할 직사각형의 x 또는 y의 최댓값이 0이면 싱크홀의 영역이 모두 True이고 모든 영역이 덮었기 때문에 0을 출력한다.
'파이썬(Python)' 카테고리의 다른 글
| [Python] 배열에 기록하여 문제 풀기 (0) | 2023.12.18 |
|---|---|
| [Python] 최장 연속 부분 수열 (0) | 2023.11.11 |
| [Python] 특정 구간의 개수 구하기 - 겹치는 지점, 겹치는 구간 (0) | 2023.10.29 |
| [Python] 진수 변환 - 2진법 표현, 10진법 표현, 진수에서 진수 변환, 아스키 코드 (0) | 2023.10.23 |
| [Python] 시간과 날짜, 요일 구하기 (0) | 2023.10.20 |